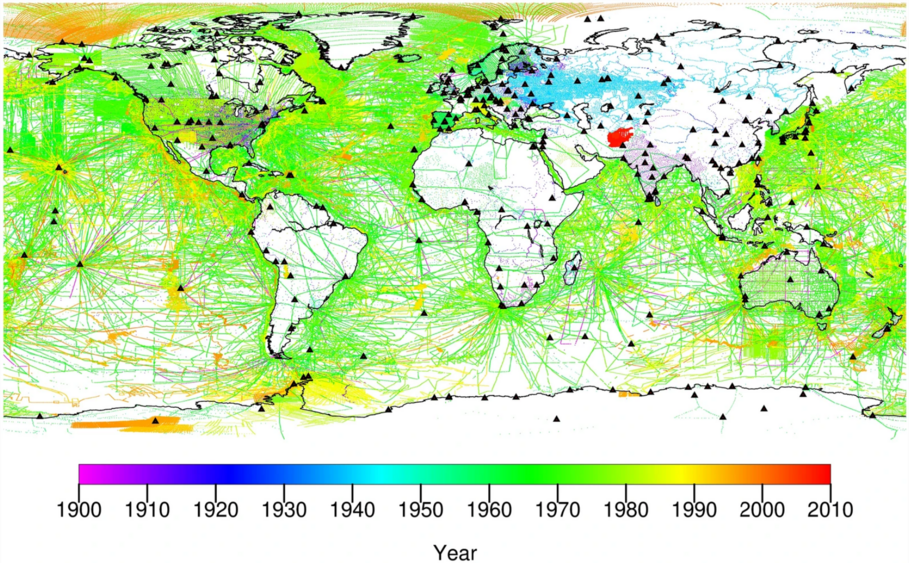
Datenassimilation (DA) ist ein Sammelbegriff für mathematische Methoden, die konsequent numerische Modelle mit Beobachtungen kombinieren. Am GFZ beschreiben unsere Modelle die geophysikalische Dynamik und die assimilierten Beobachtungen sind Erdbeobachtungen (z.B. Abb. 1). DA ist oft notwendig, da selbst perfekte Modelle auf die richtige Bahn gebracht werden müssen, um realistische Ergebnisse zu liefern. In der Regel geschieht dies durch Aktualisierung des Modellzustands, der Anfangsbedingungen und/oder der Randbedingungen des Modells mittels DA.

Wendet man die gleichen Methoden an, um einen allgemeinen numerischen Operator durch Daten zu aktualisieren, spricht man von maschinellem Lernen oder KI. Ein weiterer Vorteil von DA oder KI ist, dass die in den Beobachtungen enthaltenen Informationen genutzt werden können, um Wissen über unbeobachtete oder sogar unbeobachtbare Größen abzuleiten. Dies wird durch die Ausnutzung physikalischer oder statistischer Zusammenhänge zwischen beobachteten und unbeobachteten Variablen erreicht (vgl. Abb. 2 & 3).

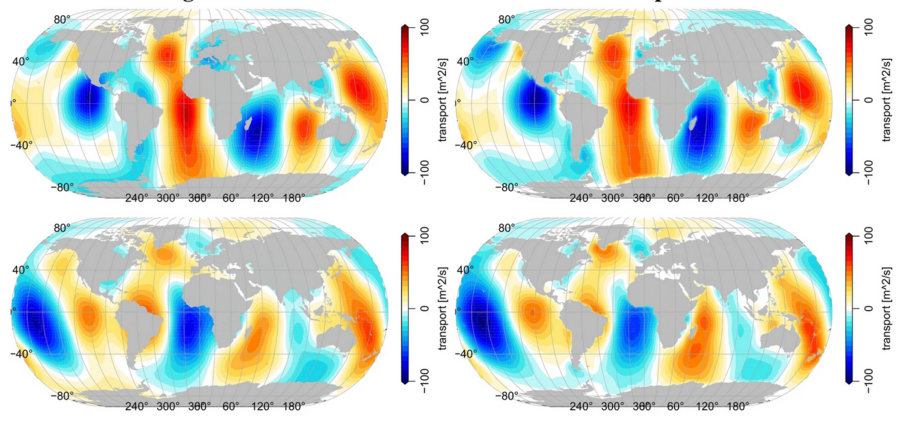
DA und AI in unserem Bereich konzentrieren sich hauptsächlich auf geodätische Beobachtungen, z. B. Erdrotation, Satellitengravimetrie und Satellitenaltimetrie [Saynisch et al., 2011a, 2015]. Darüber hinaus werden neue Technologien in so genannten Observing System Simulation Experiments (OSSE) auf ihren potenziellen Nutzen für die jeweilige Forschungsgemeinschaft getestet, wie z. B. die neu entstehende GNSS-Reflektometrie-Technologie oder Satellitenmagnetometer-Beobachtungen. 

Im Allgemeinen werden die Beobachtungen mit modernen numerischen Modellen der Teilsysteme der Erde kombiniert, z. B. Atmosphäre, Ozeane, Mantel und Kryosphäre [Neef und Matthes, 2012, Irrgang et al., 2017, Bernales et al., 2017].

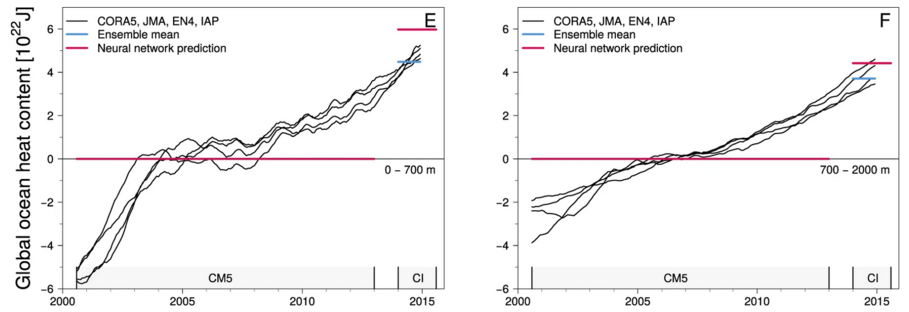
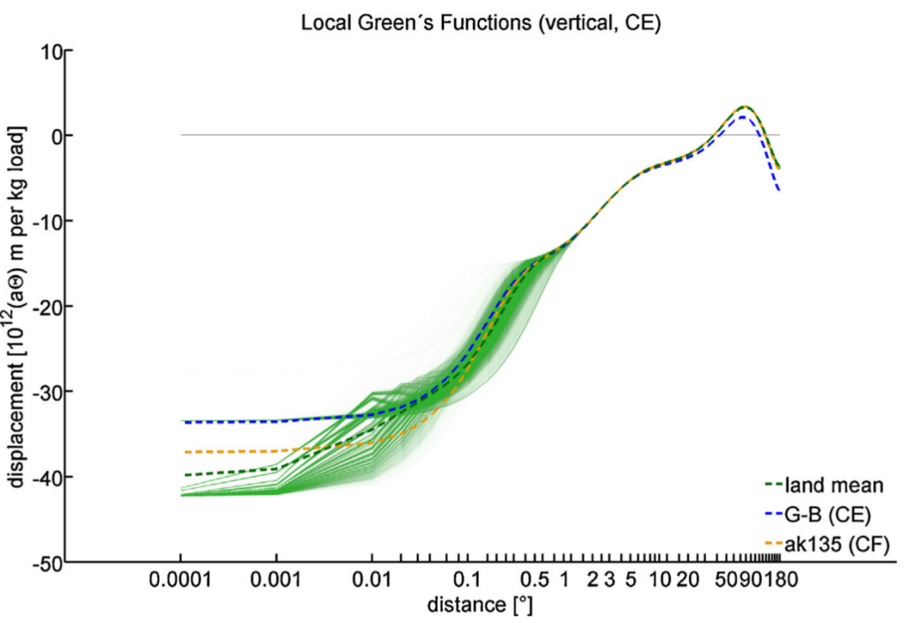
Vor einer erfolgreichen Assimilation müssen realistische Fehlerbudgets abgeleitet werden. Einerseits beschreiben diese Budgets realistische Statistiken der Beobachtungen, z.B. von GRACE [Dobslaw et al., 2016] oder GNSS-R [Semmling et al., 2016]. Andererseits müssen diese Budgets die Unsicherheiten und Sensitivitäten der verwendeten numerischen Modelle beschreiben, siehe Abb. 4 [z.B. Zhang et al., 2017, Dill et al., 2015].

Für die Modellfehlerabschätzung sind numerisch aufwendige Ensembleberechnungen erforderlich [z.B. Irrgang et al., 2016]. Im Rahmen von Benchmark-Experimenten basieren diese Ensembles idealerweise auf sehr unterschiedlichen Modellen [Saynisch et al., 2017, Sachl et al., 2017]. Die Ensemble-Informationen werden anschließend in modernen Ensemble-Kalman-Filtern verwendet [Irrgang et al., 2017]. Aufgrund der typischen Hochdimensionalität von Modellen der Erdsystemkomponenten müssen die Ensemble-Generierung und die Kalman-Filter auf kleinen, aber dynamisch optimalen Teilräumen operieren [z.B. Nerger et al., 2005].

Neben Kalman-Filter-Techniken werden in Abschnitt 1.3 auch eine Reihe von Variations- oder adjungierten Techniken verwendet [Saynisch et al., 2011b, 2015]. Je nach der spezifischen Forschungsfrage können die Modelle und die Formulierung der Assimilationsmethode regional oder global, statistisch oder variierend sein. In bestimmten Fällen werden die gleichen Beobachtungen sowohl mit adjungierten als auch mit Kalman-Filter-Techniken assimiliert, um die Robustheit der Ergebnisse zu erhöhen [vgl. Saynisch und Thomas, 2012, Saynisch et al., 2011b]. 

Im Rahmen des internationalen GEROS-ISS-Projekts konnten wir erstmals den Informationsgewinn von GNSS-Reflektometrie-Messungen für die ozeanographische Gemeinschaft demonstrieren und konkrete Empfehlungen für offene Fragen der Beobachtungsdichte und -genauigkeit geben [Saynisch et al., 2015, Wickert et al., 2016]. Im Rahmen des SMART-Cables-Projekts, das darauf abzielt, Telekommunikationskabel mit ozeanographischen Sensoren auszustatten, könnte eine Strategie für die Kabelverlegung vorgeschlagen werden, die auf der Assimilationswirkung des jeweiligen Kabels basiert. Im Rahmen des Dynamic Earth-SPP wird Pionierarbeit bei der Untersuchung des Potenzials der derzeit laufenden Satelliten-Magnetometer-Mission Swarm für ozeanische Assimilationszwecke geleistet [Irrgang et al., 2017, Saynisch et al., 2017, 2023].

Mit Hilfe von KI können die trainierten Operatoren nicht nur zur Vorhersage, zum Downscaling oder zur Invertierung geophysikalischer Daten eingesetzt werden [Dill et al., 2021, Schachtschneider et al. 2024, Jung et al., 2024], sondern auch zur Speicherung und Erkundung großer Datensätze (vgl. Abb. 5). Die in unserem Abschnitt entwickelten Methoden können darüber hinaus zur Modellierung von Situationen und Ereignissen verwendet werden, die mit traditionellen Methoden nur sehr schwer zu modellieren wären.